108. Convert Sorted Array to Binary Search Tree

题目描述：

給定一個升序排序的整數陣列 nums，將其轉換為一棵高度平衡的二元搜索樹，並返回該樹的根節點。

Example: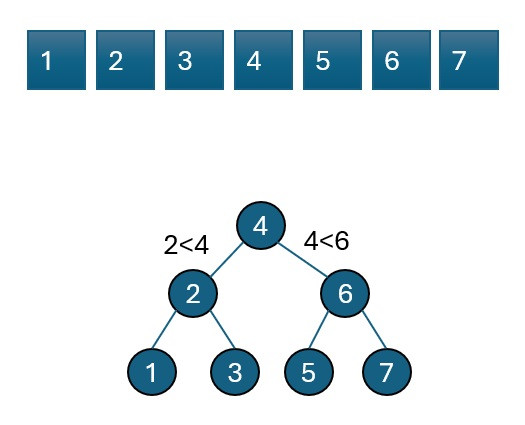

• Input: nums = [1,2,3,4,5,6,7]
• Output: [4,2,6,1,3,5,7]

解題思路:
高度平衡的二元搜索樹（height-balanced binary search tree）是指樹中的每個節點的兩個子樹的深度相差不超過一層。同時，二元搜索樹（BST）要求根節點的值必須大於其左子樹中所有節點的值，並且小於其右子樹中所有節點的值。換句話說，根節點通常是整個樹的中間值，而左右子樹的根節點則是各自子樹的中間值。

考慮到這些特性，並且題目已經提供了升序排序的輸入數組，這讓我們聯想到可以使用二元搜索法來解這個問題。二元搜索法的特點正好符合我們需要的中間點分割的思路。通過不斷地選擇中間值作為根節點，並遞迴地構建左右子樹，我們可以輕鬆構建出一棵高度平衡的二元搜索樹。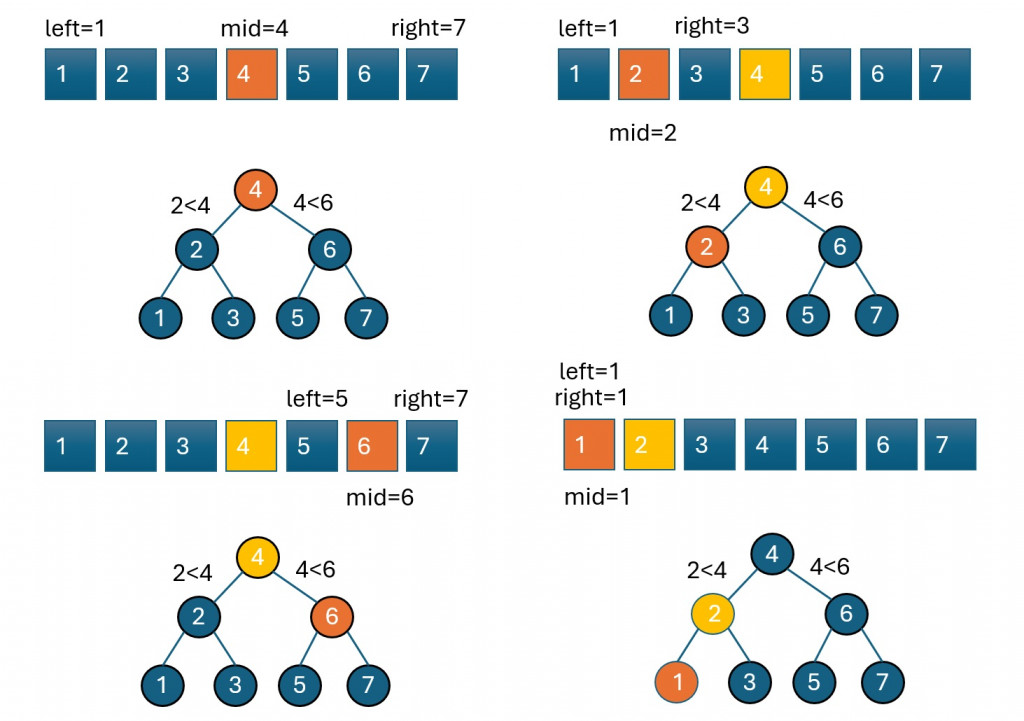

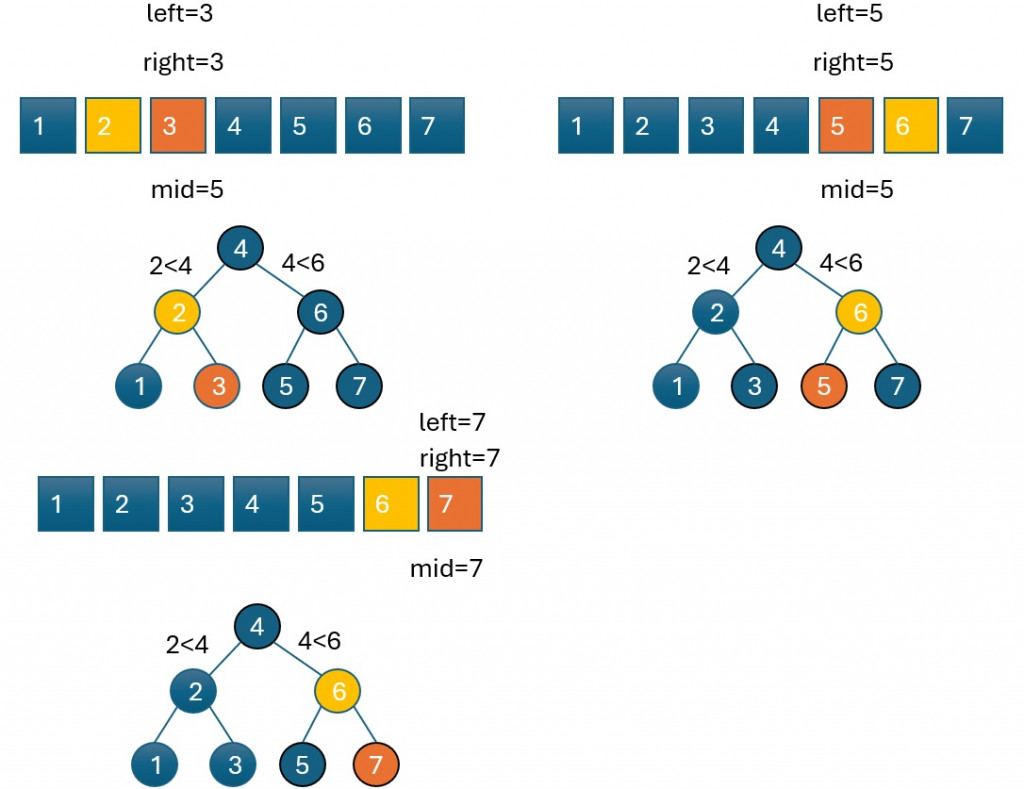
var sortedArrayToBST = function(nums) {
    if (!nums.length) return null;

    function buildBST(left, right) {
        if (left > right) return null;

        const mid = Math.floor((left + right) / 2);
        let root = new TreeNode(nums[mid]);

        root.left = buildBST(left, mid - 1);
        root.right = buildBST(mid + 1, right);

        return root;
    }

    return buildBST(0, nums.length - 1);
};

時間複雜度：O(n)，其中 n 是陣列的長度。每個元素都只會被訪問一次，因此時間複雜度為 O(n)。
空間複雜度：O(log n)，遞迴call stack的深度取決於樹的高度。在高度平衡的二元樹中，樹的高度為 O(log n)。

總結:
這道題目可以歸類為「二元搜索法」。從這道題目開始，我們第一次接觸到高度平衡的二元搜索樹。在接下來的 LeetCode 題目中，還會遇到其他類型的樹（tree）結構。通過 LeetCode 的練習，我們可以學習如何構建這些樹，並熟悉它們的遍歷方法（traversal）。

建議讀者在解題過程中，先理解每種樹的特性，然後多練習如何正確地構建和遍歷這些樹。這樣不僅能提升對樹結構的理解，還能為解決更複雜的問題打下堅實的基礎。隨著不斷的練習，你會發現自己的解題能力和程式設計技巧都在逐步提升。